An
Alternative View of Nuclear Structure
Aran
David Stubbs
Abstract
This is a description of an alternate to the standard models of nuclear structure, with a crystalline structure of diquarks and monoquarks. Nuclei were found to follow a least surface function, modified by minimizing the dipole on the nucleus. It assumes a structure to the quarks based on a theory of gravitons as low-energy tachyons, with a photon-like shell surrounding each charged structure, and each monoquark containing a proto-quark in a spherical orbit just above a pair of gravitons also in spherical orbits, with the diquark being a proto-diquark above 2 gravitons. Other fundamental particles (photons and leptons) are also proto-matter above gravitons.
This theory provides a diameter of the proton of 1.60(1) fm, and minimum base frequency of the graviton of 4.148 x 1042 cycles per second. A brief analysis of the energy and size of some other nuclei are also included. There are illustrations of many nuclei, a table of links for best fit for baryon count of 1 to 310, and graphs comparing the solution space to known isotopes.
Primary Structure
Since the atom was determined to be comprised of a nucleus surrounded by orbiting electrons late in the 19th century, many attempts have been made to describe the nucleus. Most have involved structures of baryons, either orbiting or crystalline. Some have involved quarks, again either orbiting or crystalline. This theory gives a crystalline structure of quarks and diquarks. Unlike other theories it gives an octahedral surface to the structure, except for a few very small nuclei. Again differently, it assumes Coulomb’s law holds for such a structure: producing a charged surface with ups, diquarks, and a few downs, plus a neutral interior comprised of downs and diquarks.
The consensus opinion has the proton comprised of a down quark and 2 ups quarks, while the neutron is comprised of an up quark and 2 down quarks. A minority view has the proton comprised of an up/down diquark and an up quark, with the neutron comprised of an up/down diquark and a down. Lichtenburg1 proposed that solution around 1968, possibly first.
Extending this picture, a deuteron (the nucleus of Hydrogen 2) is comprised of 2 up/down diquarks a down quark and an up quark. One arrangement of this is a 1x2x2 square of spheres: 
. Combining 2 such squares, a cube of spheres can be produced: 
. Now each of the 4 diquarks is bound to 3 monoquarks (some up, some down), and each monoquark is bound to 3 diquarks.
The cube of Helium 4’s nucleus (also called the alpha particle) can be expanded in various ways. A deuteron can be slapped on each of the 6 faces, producing a 32 sphere octahedra 
(O-16). A line of deuterons can be repeatedly slapped on a single face producing a columnar structure 
(Li-6) 
(Be-8). Another cube can be attached sharing 2 spheres of the first 
(Li-7), with further cubes attached outward on the plane 
(B-10) 
(C-13). Another cube can be attached sharing 1 sphere of the first, with further cubes attached outward 
(3 cubes: B-11). And finally, spheres can be attached willy-nilly to the surface of the cube (as long as reflective symmetry is maintained) 
(2 spheres: He-5) 
(6 spheres: Li-7).
It is readily apparent that to study every possible nucleus built from this structure is not feasible. However, some simplification is possible. It can be shown that the ideal octahedra have the least surface for a given volume of any body-centered cubic structures. This differs from the classical solution where a sphere has least surface of any solid, due to the definition of interior in the BCC case: having 6 neighbors. Unfortunately, the only ideal octahedra (those with a single sphere as each of the 6 vertices) all have parity violations: they have a center sphere, and all other spheres in the structure have a partner opposite them in the structure, so the count of monoquarks and diquarks differs. These are the odd symmetric solutions: 
. The actual deviation from ideal is much higher than 1 extra suggests, more typically there is a 3:2 ratio of the dominant type (that present on the outer layer) to the subordinate type.
Still, it is possible to work with nearly ideal octahedra. The 32 sphere octahedra built from the alpha by expansion is nearly ideal. It has 8 interior spheres, and no other structure with 32 spheres has more than that (a few are tied). The ideal octahedra would have 10 interior spheres. Other near ideal octahedra can be built by expanding other small structures. Expanding the 32 sphere octahedra called the second even symmetric case 
(O-16), with the cubic solution as the first even symmetric, by minimal expansion (only add a sphere to the surface where it is adjacent to a sphere of the original structure) produces another symmetric even solution, with 80 spheres, 48 of which are at the surface 
(Ar or Ca-40). A fourth solution with 160 spheres, 80 at the surface can be generated 
(Se or Kr-80). There is a fifth solution with 280 spheres and 120 surface 
(Ce-140), then a sixth with 448 (168 at the surface) 
(Po-224), and so forth 
(Cn-336).
Other simple structures can also build a series of octahedra. The 1x2x2 deuteron can be extended minimally to produce a 20 sphere structure (16 spheres at the surface) 
(B-10), which can be expanded to produce a 56 sphere structure (36 surface) 
(Si-28), then a 120 sphere structure (64 surface) 
(Ni-60), a 220 sphere (100 surface) 
(Pd-110), a 364 sphere (144 surface) 
(Hf-182), a 560 sphere (196 surface) 
(Cf-280), etc. These are the odd near-symmetric solution set.
The next structure produces an interesting dilemma. All the previous structures had similar charge distributions on the surface. Assuming all the surface monoquarks are ups, we get 2 hemispheres divided by any plane with the same charge on each. The 1x1x2 structure (proton) 
can also be expanded producing a 12 sphere structure with 2 interior spheres, 
(Li-6) then a 38 sphere structure with 12 interior. 
(F-19) But in this case, the 26 surface spheres of this solution have a dipole: all the monoquarks are in 1 hemisphere and all the diquarks are in the other. This can be resolved for the 2nd and 3rd layer by having a third of the surface monoquarks as downs. (And some of the monoquarks on the first 2 solutions sets would also be downs, as long as they are divided symmetrically so as to minimize dipole there). By layer 4 of this solution, having a third of the surface monoquarks as downs produces an unusually low z value (17) for a baryon count of 44. Layer 4 
(Cl-44) and subsequent 
(Ni-85), 
(Nb-146), 
(La-231) of this even near-symmetric group of solutions are not valid. These structures also have a chromatic dipole, that is, the center of the red quarks is separate from the center of the blue-green diquarks. For the symmetric cases and the odd-near symmetric the center of each structure for both types is identical, for the even near symmetric they are 1 diameter apart. Some other solutions have even higher chromatic dipole. The intensity of the chromatic dipole is the product of the distance between the 2 centers and the count of the spheres centered on them. Some derived solutions have a slight chromatic dipole (adding a single sphere each to a blue face and a red face makes a dipole).
There are also families of solutions with positive eccentricities derived from the even symmetric, just as we have looked at 2 families with negative eccentricities. A 2x2x3 
structure can be extended to form a set of near-symmetric solutions. Similarly the 2x2x4 or the 2x3x3 core 
can be expanded. We can also have solutions with mixed eccentricities: 1x2x3 
or 1x2x4 
as a core. Solutions with all dimensions more than 2 can be treated as cousins to those with all small dimensions, but the 3x4x4 and 4x4x4 
cases were looked at separately. Extensions to these were sometimes valid base cases.
The solutions with stretching along a plane are herein called Skew, and like the eccentric solutions they provide numerous bases for families of structures. Skew can exist in 1
, 2
, or all 3 
planes. Each of these can be of any degree, so a S123 
solution is possible. Each of these generates a family of solutions. However, only solutions with relatively small skew correspond to base state isotopes, so most can be ignored. Additionally, skew in a plane can be combined with eccentricity in the perpendicular dimension: 
. These hybrid solutions turn out to have a parity violation if the degree of eccentricity is odd. Stretching along a diagonal also often causes parity violation. A pair of cubes sharing a single sphere represents 15 total spheres, so the count of diquarks and monoquarks can’t be the same. 3 cubes in a row is the minimum valid solution for such a diagonal. Diagonals from trimming or extending a solution on 2 faces often exist as well.
In addition to all these base cases and their families, the solutions with spheres added here and there have to be taken into account. Fortunately, these routinely have more surface than the base structure from which they are derived. However the derived solutions may be the least surface for a baryon count. It was found that adding a triangle of spheres to a pair of faces made the best improvements, adding a minimum amount of surface for the maximum interior. In some cases, for example the odd near symmetric, it is necessary to add to 4 or 8 faces (to maintain reflective symmetry) since the face opposite is of the same type in those cases.
Sadly, adding to 2 faces (or even 4 or 6) often increases dipole sharply. If the base case has low dipole, this can bring the derived solutions to high dipole. Adding to all 8 faces rapidly increases the surface. For example: starting from the even symmetric case layer 5, the surface has 60 monoquarks and 60 diquarks symmetrically distributed (8 triangles of 15 spheres). Adding to any 2 faces reduces the symmetry, but typically maintains the same maximum z of 60 for low dipole. (Adding a sextet to 2 faces gives 27 of the reduced type and 36 of the enhanced, maximum z=2*(36*1/3+27*2/3) using the more common type as diquarks which have a charge of 1/3, and the lesser as ups with a charge of 2/3 and adding a balancing charge in the monoquark dominated hemisphere. Adding a smaller amount slightly increases the maximum z, adding a larger amount slightly lowers maximum z.) Similarly adding to 4 faces maintains the 60 limit. However if we add to 6 faces, the limit slowly rises (a third as fast as the increase in surface), and if we add to all 8 faces it goes up evenly with the increase in surface. When the base case had moderate dipole, adding to 2 or 4 faces can reduce dipole.
Most of the skew families of solutions and some of the eccentric have moderate to high dipole for the base case. This is not a problem with small nuclei, since some surface downs are needed to reach ideal z, but with large nuclei where the surface is all ups and diquarks, it is difficult to find a low dipole solution. Since the octahedra are defined by 7 planes it is necessary to calculate the dipole from each (3 planes defined by the vertices, 4 defined by pairs of faces). For high baryon count, many high-dipole solutions can be generated with less surface spheres than low dipole solution. For example, a 259 baryon count with 92 surface monoquarks can be generated from the even near-symmetric case, but it has a maximum z of 80. Ideal z at that point is around 101, which is quite a shortfall.
Unioning together all the plausible structures defined so far, an overall solution space can be generated. This was visualized by graphing the normalized ratio of surface to interior of each solution point versus baryon count. The base of the graph showed a jagged edge, with local minima at each complete structure surrounded by V’s of derived solutions, and a regional minima periodically corresponding to the odd-symmetric case and the even near-symmetric case. Indeed, the even solutions formed a recurring set of ridgelines of solutions, while the odd solutions formed a set of odd ridgelines. Comparing this solution space against the known isotopes, it was found a simple mapping was possible. Each stable isotope could be built from a valid solution (one with low dipole, good parity, and small surface) with a few surface downs. The worst cases (starting with Calcium 46) each required 8 surface downs (2 per monoquark face of the octahedra).
While it is possible to build a solution with least surface for large isotopes, solutions with more than least surface tend to be stabler. This introduces a concept of “fluffiness”, the addition of spheres beyond the near-ideal octahedra to bring it closer to a sphere. For example:
|
Even |
Extended |
Extended |
Each of these has the same basic shape: A near ideal octahedra with no eccentricity and no skew. But the right 2 are closer to a sphere and correspond to known isotopes (Radium 228 and Fermium 252), while the leftmost represents Polonium 224, which is 4 beyond the heaviest known isotope of Polonium. Fluffy solutions often have lower moments of Inertia than solutions with least surface. From this, and the known behavior of the existing stable isotopes, an ideal z function was roughed out. This agreed pretty well with previous predictions of z to A mapping. Based on the observed behavior of heavy isotopes, cases where z is 2 less than the ideal often produces more stable isotopes than the actual z. So for example the ideal z at baryon count of 238 is 94 (where energy per baryon is lowest), but z of 92 is most stable. This leads to some added jumpiness in the z:A mapping of relative stability.
There are several measures of the central tendency typically observed. The simplest, used as primary here, is the least surface. Other measures include least maximum diameter, highest total bond count, and least moment of inertia. In cases where 2 solutions have the same surface, and dipole is not a factor, the solution with the least maximum diameter would tend to be preferred. This should equate to lowest moment of inertia, but in cases where it does not that would be a tie-breaker. As an example, for small and medium nuclei, the even symmetric solutions (S000) and the thin skew 1 solutions (T001) each have the same surface. The symmetric has more dipole, but a little less maximum diameter. In that region, the symmetric is superior. For large nuclei, the zero dipole of the thin skew is most important, since there aren’t any surface downs to counteract the dipole of the symmetric.
The Euclidean length of a nucleus can be calculated from the simpler Manhattan length. For the 4 simplest cases, the even symmetric, odd near-symmetric, even near-symmetric, and odd symmetric, the Manhattan length of all 4 pairs of faces is equal at a given layer. A simple formula for each type was derived with mL the Manhattan length, and L the layer number. For the even symmetric, mL=2L+1. For the odd near-symmetric, mL=2L. For the even near-symmetric, mL=2L-1. For the odd symmetric mL=2L-2. These lengths are from the center of a sphere to the center of the corresponding sphere on the opposite face, assuming all spheres are identical in size in terms of sphere diameters. Cases with 1 size for the monoquarks and another size for the diquarks can also be calculated, where the unit is the mean diameter. It should be recalled that the gross size of the nucleus is the largest Euclidean diameter plus the distance from the center of the spheres in question to the actual surface. This is 2 radii, which may be the diameter of the larger type or the mean diameter depending on the geometry.
From the Manhattan length, calculating the Euclidean length involves finding the combinations that add to the Manhattan length. In the simplest case, the even symmetric, the individual lengths are odd integers. Layer 1 is 1+1+1=3. Layer 2 is 3+1+1=5. Layer 3 has either 5+1+1 or 3+3+1=7. Layer 4 has 7+1+1 or 5+3+1 or 3+3+3=9. Euclidean lengths are thus √(12+12+12)= √3 for layer 1, etc.. The center of the face has lengths most equal.
Symmetric cases with 3 different integers correspond to 6 spheres at a distance per face, those with 2 different integers to 3 spheres at a distance, and cases with 3 identical integers have a single sphere at the distance. Note: the even symmetric has odd lengths while the odd symmetric has even lengths. For the near symmetric, with a mix of odd and even integers, solutions are either 1 sphere at a distance per face (if 2 components are equal), or 2 spheres at the distance (if all 3 components are different).
More complicated formulas can be derived for the other families of solutions. For instance the D-1 solutions have 2 faces at 2L+1 and the other 6 faces at 2L+3. Although D-1 solutions have such high chromatic dipole they can generally be ignored. Skew solutions can have 2, 3, or 4 sets of Manhattan lengths. Eccentric and hybrid solutions with stripes (that is with wide edges) have a separate Manhattan length for each stripe, in addition to the lengths calculated for the various faces.
See also the Size of Nuclei.
Graphs
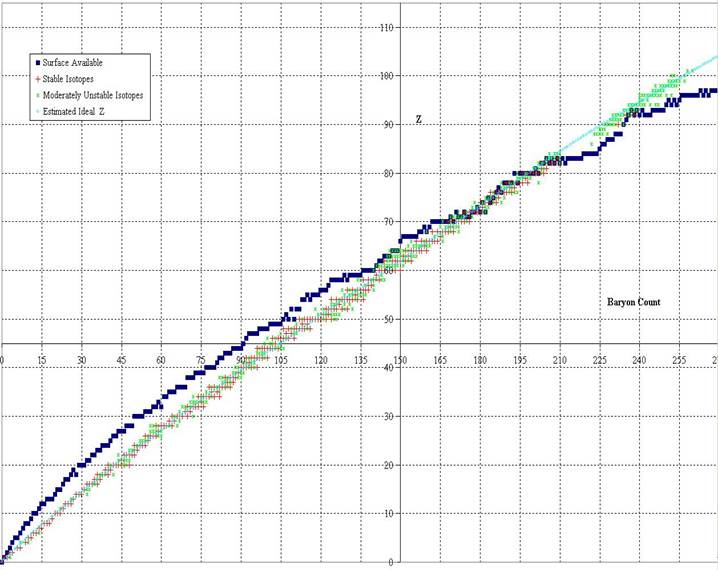
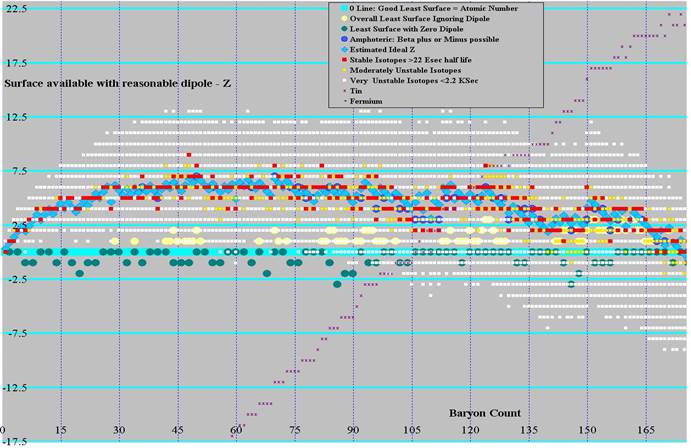
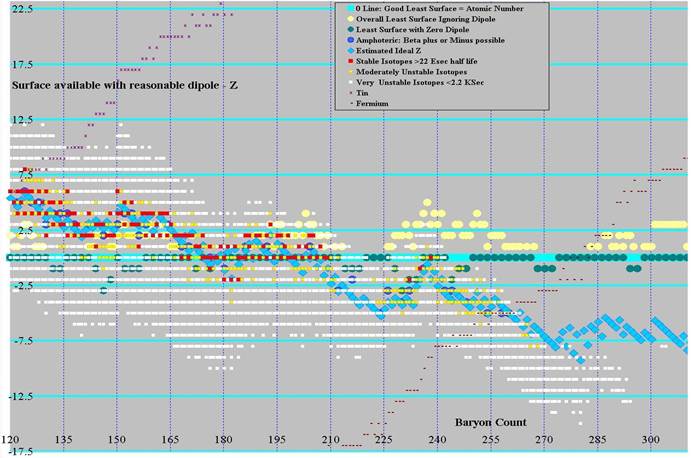
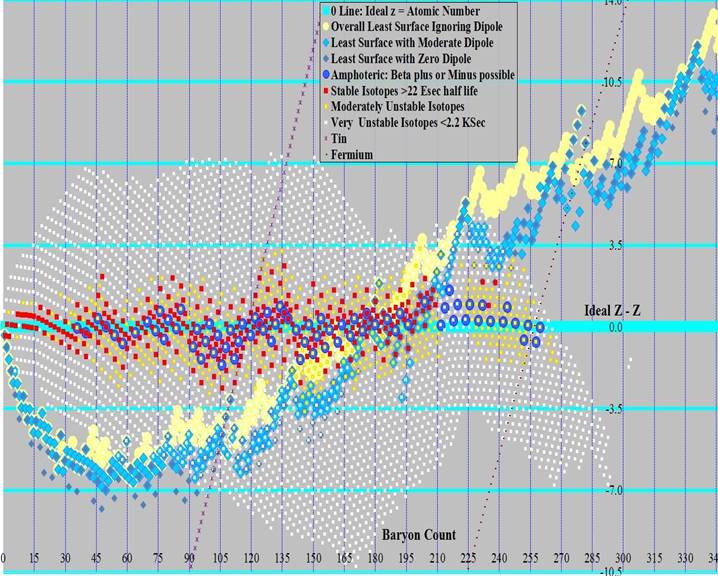
Graphs were produced showing the relationship among least surface, ideal z, and the known isotopes. The first graph of baryon count versus z uses a moderate least surface, where dipole can be removed with 4 or fewer surface downs. The second and third graphs shows the difference between this least surface value (turquoise line at the center) and 1) the known isotopes (red for stable(ish), orange for moderately unstable, white for very unstable), 2) ideal z (blue diamonds), 3) amphoteric isotopes (those that can either gain or lose an electron to become stabler) as blue circles, 4) least surface ignoring dipole (pale yellow circles), and 5) least surface where no dipole exists (only possible for even baryon count and even z) as dark green circles. Graph 2 covers baryon count 0 to 175 and graph 3 covers 120 through 310. The same ideal z was used on all 4 graphs, the jumpiness on 2 and 3 are from the jumpiness in least surface. Graph 4 shows Ideal z as the center line, covering A of 0 through 345.
Conclusion
It is interesting to note that all stable isotopes under atomic weight 176 can be built from the least surface solution with moderate dipole. A half-dozen stable and near stable isotopes from 176 through 238 use slightly more surface than the least, and no stable isotopes requires more than 2 extra ups beyond the least surface structure with moderate dipole. It should be noted that curvature on the least surface flattens out leading up to the regional minima (see baryon counts of 80, 110, 140, 182, 224, 280), with the odd ridges (110, 182, 280) bifurcating (surface sphere count on the even isotopes flattening out, odd not).
In order to visualize these structures, software was used to produce 3-dimensional images, first in a lab at the school, then with Google Sketchups. In between, physical models were built using chemical modeling kits. Images from all 3 are available online.
Below is a table of links to the Google Sketchups of the best fit solution found thus far. As these were generated manually, some cases may not be actual best fit. Each row has baryon count, and 3 solution cells: least surface ignoring dipole, least surface with dipole that can be corrected with 4 or fewer surface downs, and least surface with zero dipole. Only even baryon counts have solutions in the final column. The first solution cell may have many solutions with the same surface, from least dipole to most. The second cell has only 1 solution with the minimum dipole for the surface (or a few if there are ties). In a few cases for large nuclei where the ideal z is above the least surface some example solutions that were pretty are included. These are more likely to match actual isotopes than the least surface cases. The illustrations linked to all have red monoquarks. All 3 possible color schemes 
should be equally likely, red monoquarks and blue-green diquarks was chosen for aesthetic reasons.
Since the point at which dipole is minimum depends on the particular structure, there are some cases where a trio of consecutive solutions based on 2 different structures are stable (or at least close). Generally, the existence of dipole adds a wave function to the energy, with 2 low dipole solutions having a higher dipole solution in between (where a single surface down becomes an up, creating a disparity). On a few occasions where the energy is relatively flat over a wide range of z values 3 stable cases z, z+2, and z+4 can all exist (A=124 for example). In those cases ideal z is near the middle of the range. The actual value of ideal z depends on the balance between the energy from mutual repulsion of the surface charges, and the lower “rest” energy of the ups on the surface.
An additional constraint to nuclei size is Dirac’s limit. Maximum z is less than 137, with a practical limit around 132. Theoretic work was done on nuclei as large as 890 baryon count, but the heaviest practical within the limit is less than half that large.
Several other effects also need to be taken into account. Large nuclei have significant moment of Inertia. This can be minimized by bringing the surface closer to the center of mass (making the structure more spherical). However, this increases the surface sphere count. Also, the number of bonds in an octahedral structure is less than the maximum possible. A rectilinear structure has more bonds among the spheres, but again a larger surface. Finally, an octahedral structure typically has more charge surfaces than a spherical structure (but less than a cubic structure). For medium to large size nuclei it may be necessary to look at many alternatives to find an exact solution with low total surface, few charge surfaces, low moment of inertia, low dipole, and high bond count. This analysis only looked at least surfaces and low dipole in any detail.
References
D.B. Lichtenburg, L.J. Tassie, P.J. Keleman. Quark-Diquark Model of Baryons and SU(6). Phys. Rev. 167, 1535-1542 (1968).
J.E.Horvath. Stable Diquark Matter. Phys. Lett. B 3-4, 412-416 (1992).
R. Rapp, E. Shuryak, I Zahed. Chiral crystal in cold QCD matter at intermediate densities? Phys. Rev. D 63, 034008 (2001).